こんにちは!個別指導WAMです(^^)/
今回は【三角形・直角三角形の合同条件】についてお話します。
中学生で習う単元の一つに「合同な図形」があります。
皆さんはその条件を覚えていますか?
「条件とは?」「どの部分を見ればいいの?」と不安になっている方もいるかもしれません。
数学では公式や定理などの暗記が必須となりますが、証明問題を解くうえでも重要となります。
今回は、三角形・直角三角形の合同条件について詳しく見ていきましょう!
Contents
合同な図形とは?
合同条件
合同条件とは、ふたつの図形の形と大きさが同じであり、平行移動・回転移動・鏡映によってふたつの図形が重なる図形のことを指します。
相似条件との違い
合同条件と間違いやすい条件に「相似条件」があります。
相似条件とは、同じ形で大きさの違う図形のことを指します。
相似の図形は、対応する辺の「比」がすべて同じになります。
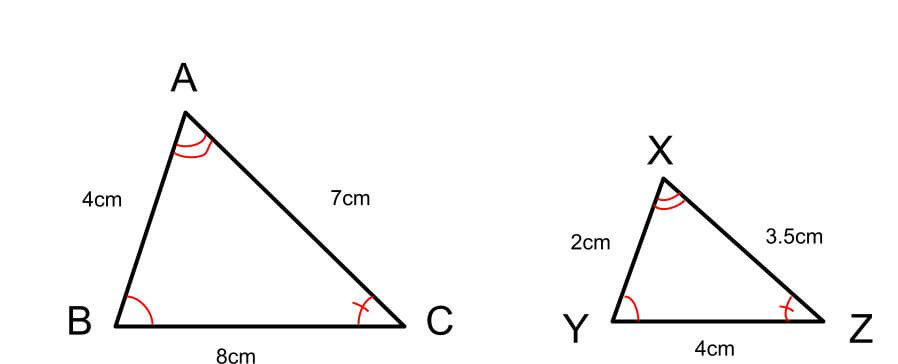
つまり、
合同条件:形も大きさも同じ図形
相似条件:形は一緒だけど大きさが違う図形
という違いがあります。
三角形の合同条件
三角形の合同条件
三角形の合同条件は3つあります。
①3組の辺がそれぞれ等しい
②2組の辺とその間の角がそれぞれ等しい
③1組の辺とその両端の角がそれぞれ等しい
①~③のうち、ひとつでも成り立っていたら「合同な図形」と言えます。
どの条件も「角と辺を合わせて3か所が等しい」ということがポイントとなります。
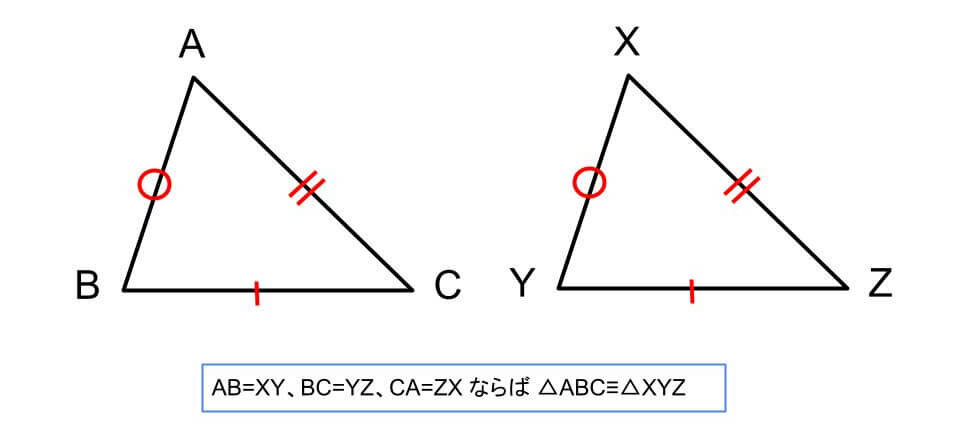
条件①3組の辺がそれぞれ等しい
3組の辺の長さが決まると三角形の形は1通りとなるため、この条件を満たすと2つの三角形は合同であると言えます。
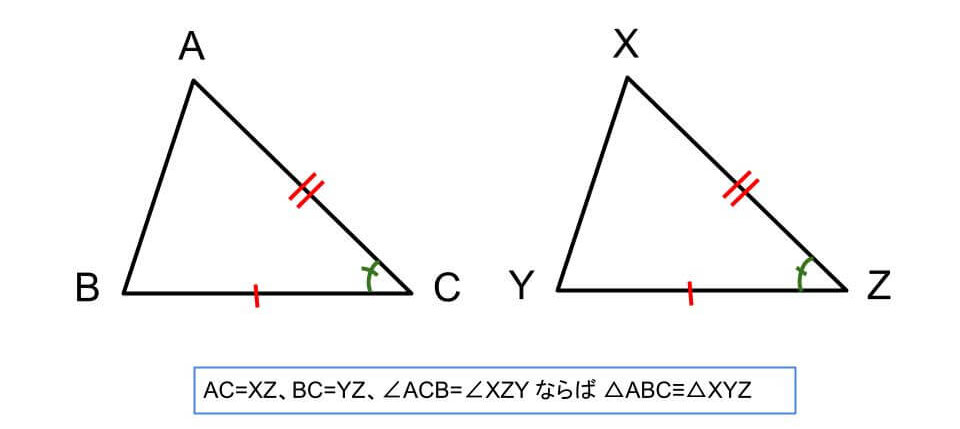
条件②2組の辺とその間の角がそれぞれ等しい
2組の辺の長さとその間の角の大きさが決まると三角形の形は1通りとなるため、この条件を満たすと2つの三角形は合同であると言えます。
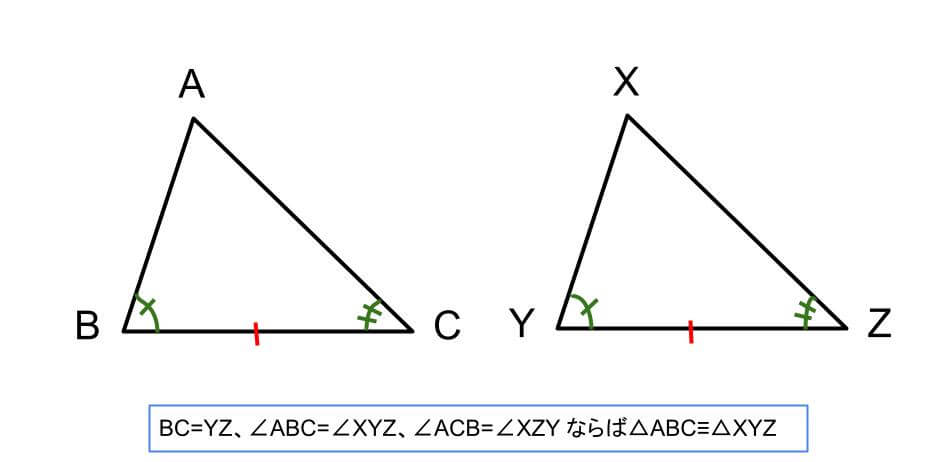
条件③1組の辺とその両端の角がそれぞれ等しい
1組の辺の長さとその両端の角の大きさが決まると三角形の形は1通りとなるため、この条件を満たすと2つの三角形は合同であると言えます。
直角三角形の合同条件
直角三角形の合同条件
直角三角形の場合にも三角形の合同条件を適用することができますが、「直角」を持つという性質により独自の合同条件があります。
①斜辺と1つの鋭角がそれぞれ等しい
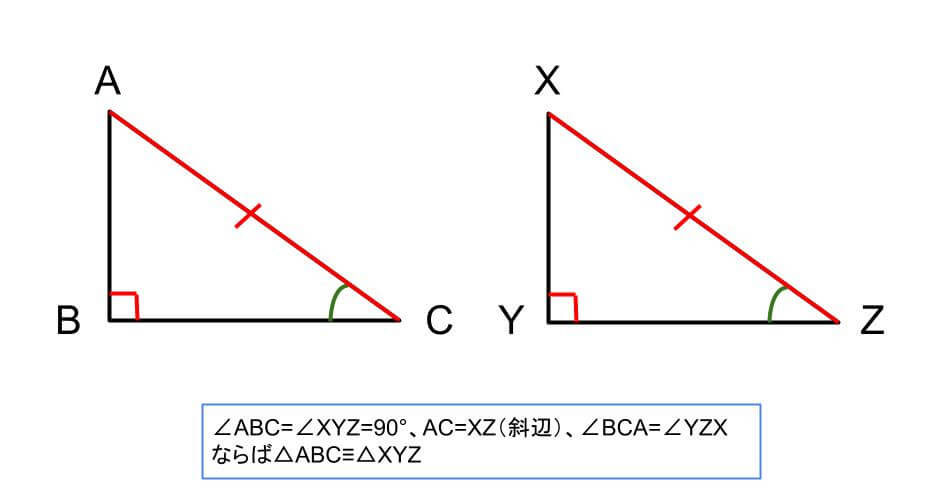
②斜辺と他の1辺がそれぞれ等しい
条件①斜辺と1つの鋭角がそれぞれ等しい
直角三角形で、斜辺の長さと1つの鋭角の大きさが決まるともう1つの鋭角の大きさも決まります。
つまり、斜辺の長さと両端の角の大きさが決まることにより三角形の形は1通りとなるため、この条件を満たすと2つの三角形は合同であると言えます。
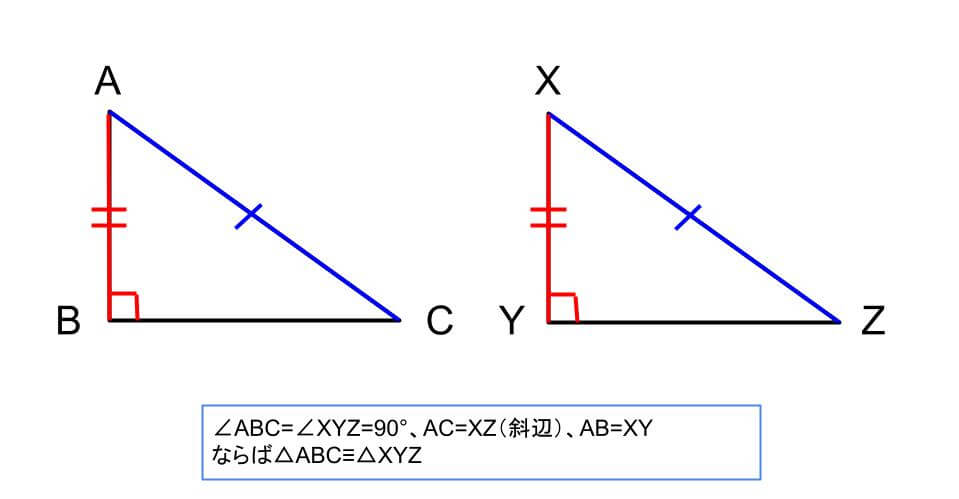
条件②斜辺と他の1辺がそれぞれ等しい
直角三角形で、斜辺と他の1辺の長さが決まると合同を証明することができます。
この2つの直角三角形を裏返して、直角と辺の長さが同じ部分を合わせると下記のように二等辺三角形ができます。
二等辺三角形の底角は等しいため、もう1つの辺の長さもしくはもう一つの鋭角の大きさが決まります。
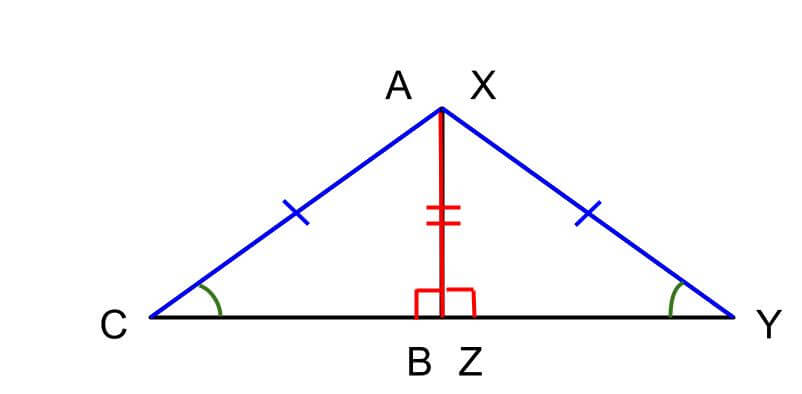
つまり、2組の辺の長さとその間の角の大きさ、もしくは1組の辺の長さとその両端の角の大きさがそれぞれ等しくなることにより、三角形の形は1通りとなるため、この条件を満たすと2つの直角三角形は合同であると言えます。
間違えやすい合同条件のポイント
3つの角が等しい=合同ではない
似たような条件となっているため「3つの角が等しいと合同である」と間違えて覚えてしまうことがあります。
合同は、形も大きさも全く同じ関係を表します。
3つの角が等しいだけだと、辺の長さが変わったときに大きさの異なる図形となってしまうため、合同であるとは言えません。
「 “それぞれ” 等しい」が重要
合同条件について回答する際は、必ず「それぞれ」という文言が必要になります。
『〇〇がそれぞれ等しいので、△△
したがって、合同な三角形の××は~~』
というような解答をしなければいけません。
「それぞれ」がないと不正解となってしまうため注意しましょう。
解答の書き方の順番をそろえる
三角形(△ABC=△DEF)や角(∠ABC=∠DEF)、辺(AB=CD)などは、それぞれの図形の対応している頂点や辺を同じ順番で書きましょう。
同じ順番で書くことにより、三角形の形をよりイメージしやすくなります。
【例題】合同証明の問題を解いてみよう
それぞれの合同条件と間違えやすいポイントを踏まえて、ここで問題をひとつ解いてみましょう。
【例題】
下記の図で、∠ACD=∠ADC、AB=AEであるとき、∠BCE=∠EDBを示せ。
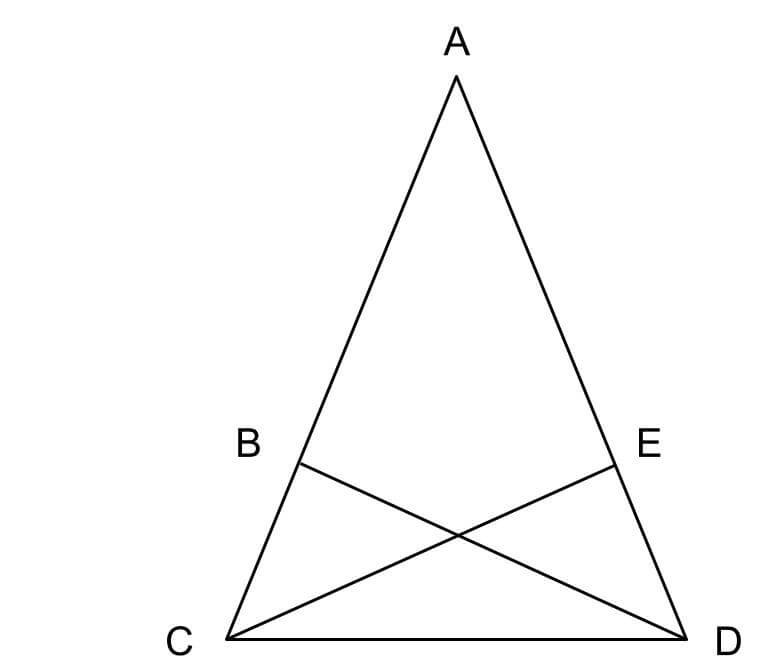
《証明》
△ACEと△ADBにおいて
∠ACD=∠ADCより、△ACDは二等辺三角形であるから
AC=AD …①
仮定より、
AB=AE= …②
また∠Aは共通している。
つまり、
∠CAE=∠DAB …③
①~③より、2組の辺とその間の角がそれぞれ等しいから
△ACE≡△ADB
したがって、合同な三角形の対応する角は等しいため、
∠ACE=∠ADB
つまり、
∠BCE=∠EDB
《証明終了》
今回の問題では、∠BCE=∠EDBを示すために△ACE≡△ADBの証明をしました。
答えを導き出すためには、問題文にあるヒント(仮定)からどの三角形の合同を証明するのが良いか判断することがポイントとなります。
様々な問題に触れることでパターンが分かってくるので、慣れるためにも問題演習をたくさんこなしましょう!
まとめ
いかがでしたか?
中学生で習う三角形・直角三角形の合同条件は、高校生で習う内容の基礎となっています。
発展的な内容を理解するには、基礎をしっかりと身につけていることが大前提となります。
合同条件について、今回のコラムを読んで
「やっぱり合同条件は苦手だな」
「相似条件との違いがイマイチ分からないな」
「教科書を読んでも自分ではよく分からないな」
「合同条件についてもっと知りたいな」
と、思った方はぜひ一度個別指導WAMへご相談ください!
苦手を克服し、学習の理解を深めるお手伝いをさせていただきます。









