こんにちは!個別指導WAMです(^^)/
今回は、【比例と反比例】についてお話したいと思います。
中学校の数学で「比例と反比例」を習いますね。
この「比例と反比例」は日常生活でも使う身近な存在ですが、「習ったけどイマイチ理解できていない」「苦手意識がある…」という人もいると思います。そんな方は、ぜひこの記事を読んで勉強の参考にしてみてください。
比例と反比例
比例とは
比例とは、一方が2倍、3倍となる時に、もう一方も2倍、3倍になる関係のことです。
例えば、1本100円のペンを買う場合、購入するペンの本数が2倍、3倍、となると金額も同じよう2倍、3倍となっていきますね。
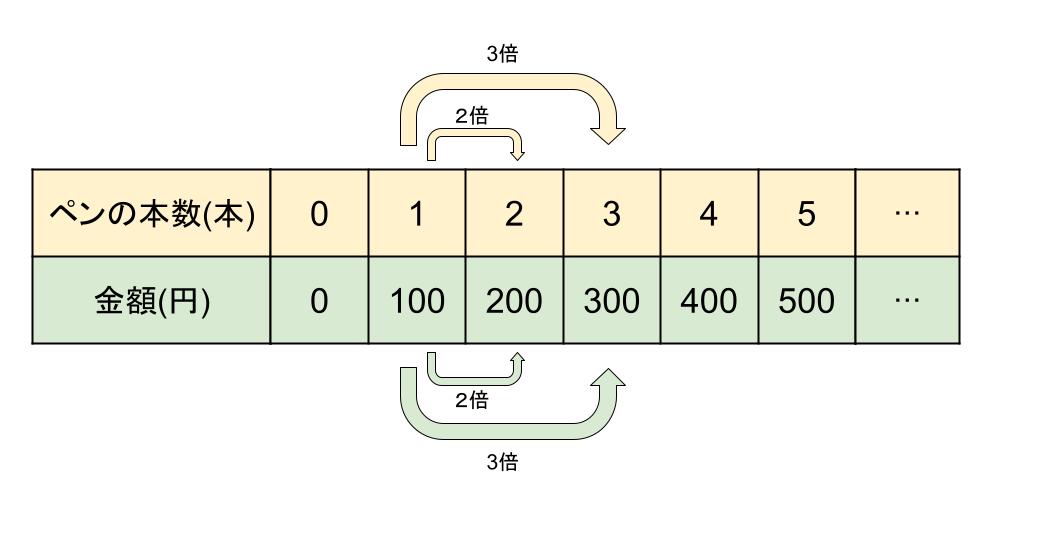
比例の関係を式で表すと《y = ax (aは0ではない定数)》となり、『a』のことを「比例定数」と呼びます。
先程のペンの例えで考えると、ペンの本数が『x』、金額が『y』です。
『y』の金額は、ペン1本分の金額100円と買うペンの本数を掛けると合計金額になるので、これを式で表すと
y = 100x という式が成り立ちます。
この式では、比例定数は『100』ということになります。
反比例とは
反対に反比例とは、一方が2倍、3倍となる時に、もう一方は1/2倍、1/3倍になる関係のことで、比例の逆数になります。
例えば、24本のペンがあるとします。この24本のペンを売り切る場合、販売日数が1日なら1日あたり24本、2日なら1日あたり12本、3日なら1日あたり8本…と日数が2倍、3倍となると、1日あたりの販売本数が1/2倍、1/3倍となっていきますね。

反比例の関係を式で表すと《y = a/x》となり、『a』のことを「比例定数」と呼びます。
先程のペンの例えで考えると、販売日数が『x』、1日あたりの販売本数が『y』です。
24本を2日で販売する場合、『y』にあたる販売本数は、24÷2 =12本となります。
これを式で表すとy = 24/x という式が成り立ちます。
この式での比例定数は『24』ということになります。
y = a/x を a について解くと
a = x × y となるため、上の図を見て分かるように、販売日数と1日あたりの販売本数を掛けると
1×24、2×12、3×8、4×6…すべて24となります。
比例と反比例のグラフ
比例のグラフ
グラフでは横軸をx軸、縦軸をy軸といい、x軸とy軸が交わる点を原点といいます。比例のグラフは、必ず原点(0)を通る直線となります。
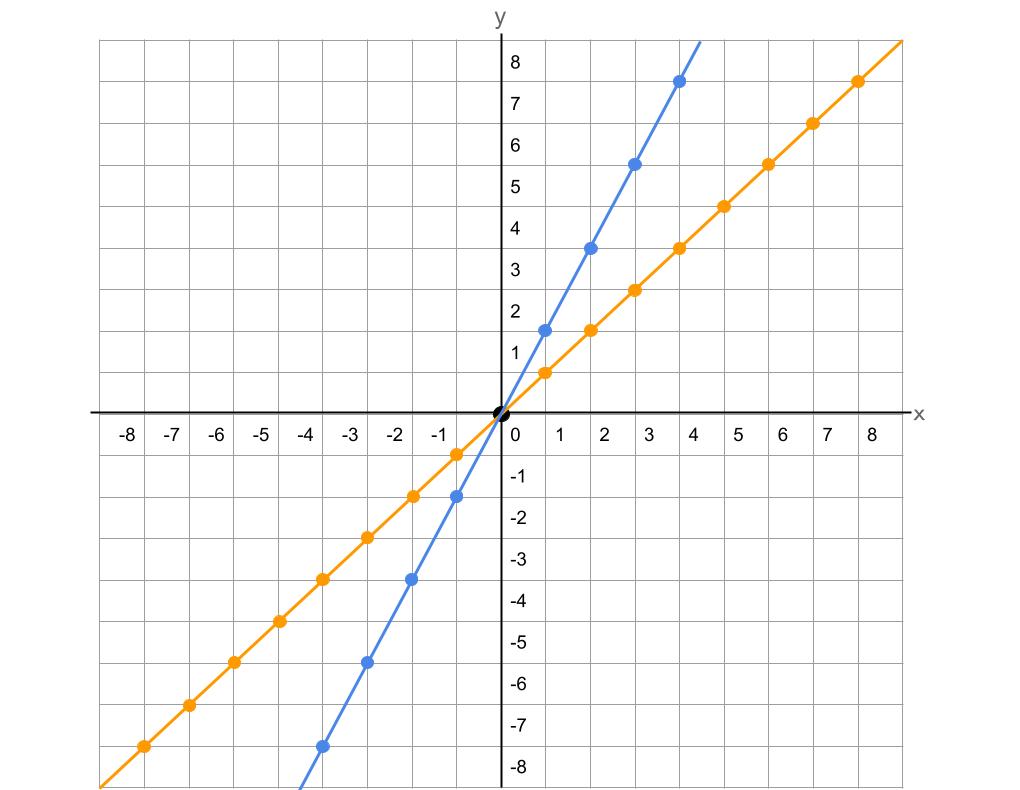
上は、y = x と y = 2x のグラフです。
グラフを見ると分かりますが、『x』が 0 の時、y = 1 × 0、y = 2 × 0 となるため、必ず原点(0)を通るということになります。
下の図は、それぞれのグラフの座標です。
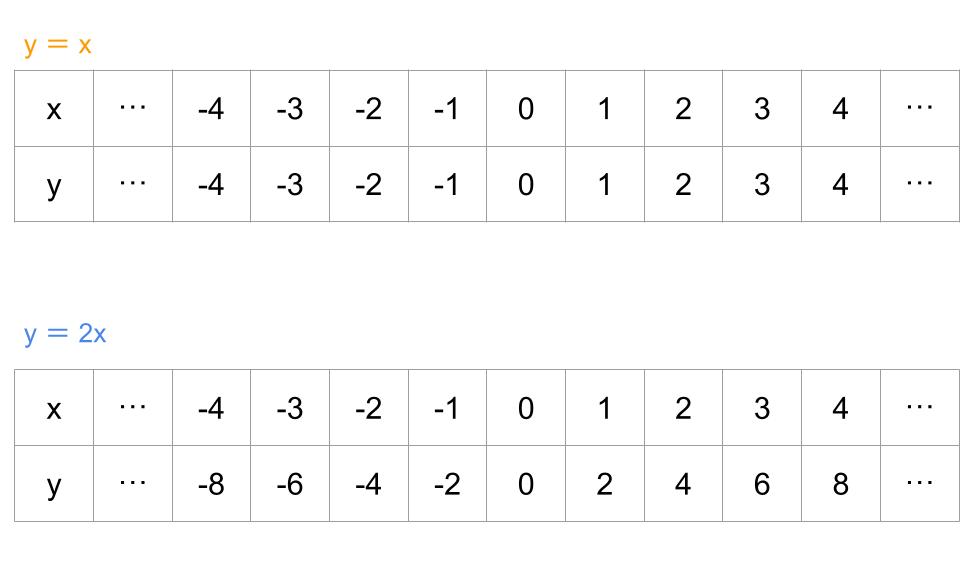
座標を答える場合は、(1,1)、(-3,-6) など、左にx座標を、右にy座標で表します。
反比例のグラフ
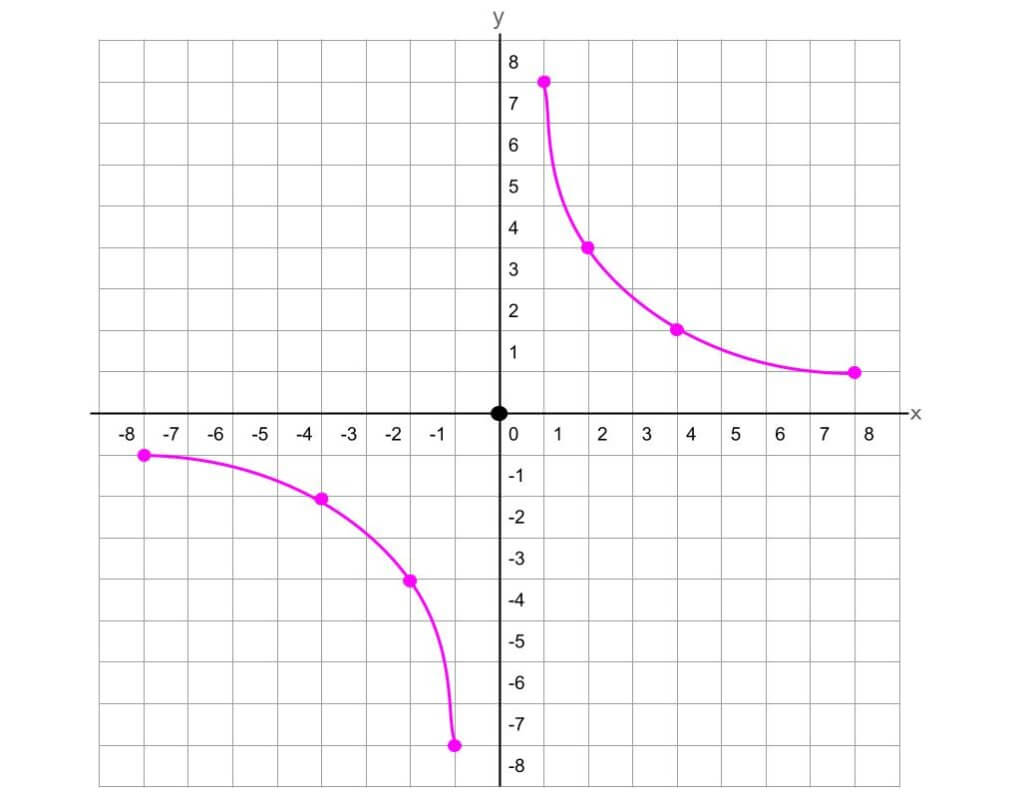
反比例のグラフも、比例のグラフと同様に横軸をx軸、縦軸をy軸といい、x軸とy軸が交わる点を原点といいます。反比例のグラフは直線ではなく、1つの式につき2つの曲線からなる双曲線と呼ばれるグラフとなります。反比例のグラフが通る座標をたくさん見つけて、曲線を書く必要があります。
上は、y = 8/x のグラフです。
分母である『x』に0 を入れることができないため、反比例のグラフは原点(0)を通りません。なぜ曲線が2つできるのかは、座標を見ると分かりますね。
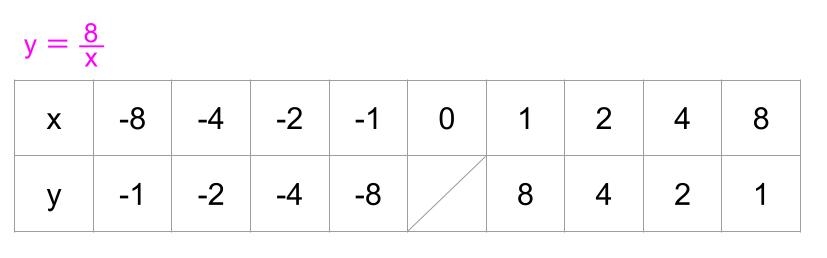
反比例のグラフを書くときの注意点は、点と点の間を滑らかに結ぶことと、x軸とy軸に線をつけないようにすることです。
練習問題に挑戦しよう
《問題》グラフ上の座標を示しなさい。
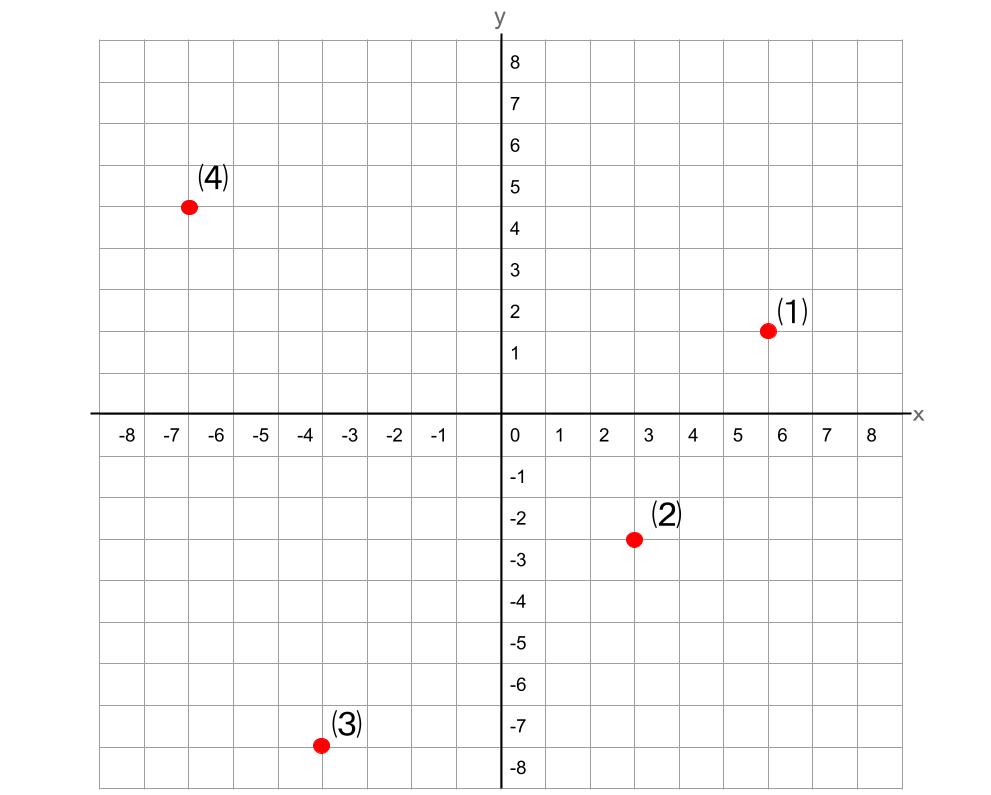
《答え》
⑴ (6,2)
⑵ (3,-3)
⑶ (-4,-8)
⑷ (-7,5)
《問題》y = -3x のグラフを書きなさい。
《答え》
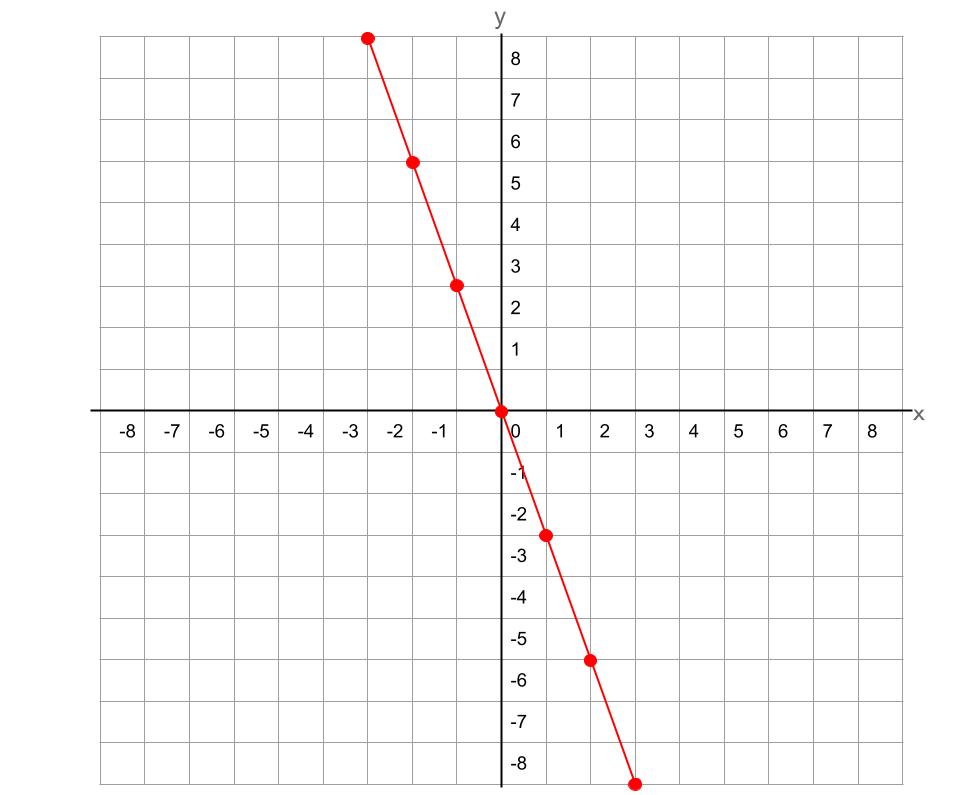
比例定数が負の場合でも、グラフの書き方は同じです。
比例定数が正の場合は、原点を通って右肩上がりのグラフになり、比例定数が負の場合は、原点を通って右肩下がりのグラフになります。
《問題》次のグラフを式で示しなさい。
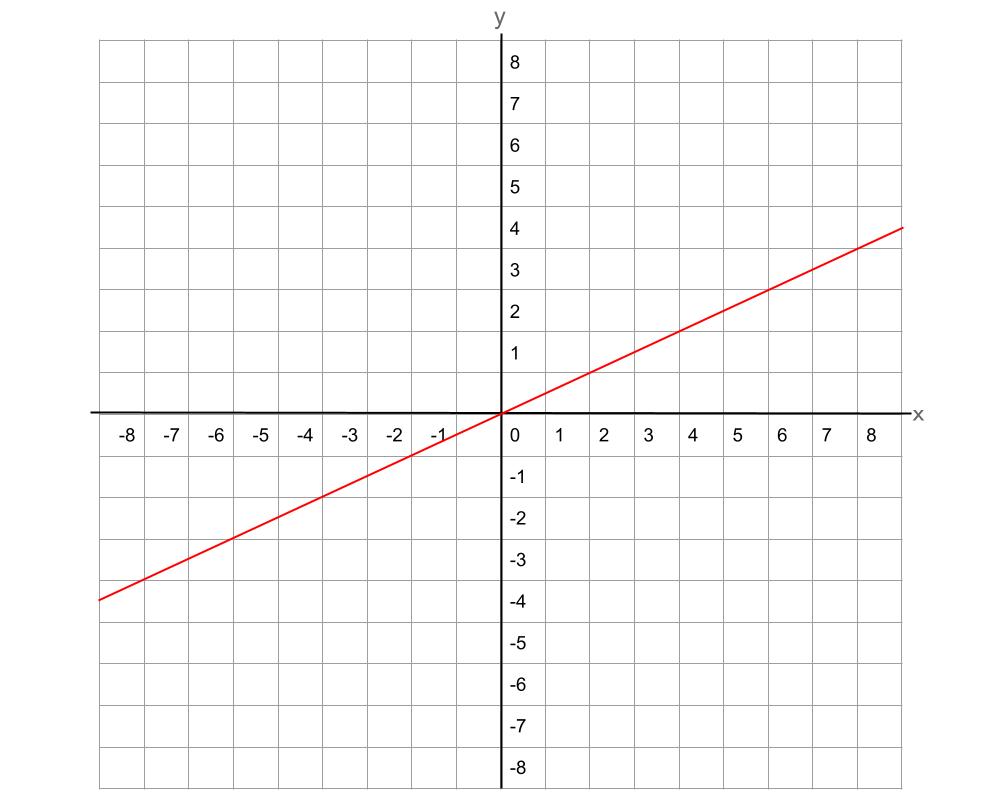
《答え》
グラフを確認すると、原点を通った一直線になっているので、比例のグラフであることがわかります。
比例関係の式は y = ax なので、この式をaについて解くと a = y/x となります。
グラフのx座標が2の時y 座標は1(2,1)、x座標が4の時 y座標は2(4,2)ということが確認できます。
a = y/x に先程確認した座標を入れると
a = 1/2 となり、比例定数が1/2であることが分かります。
よって答えは y =1/2x となります。
まとめ
いかがでしたか?
「比例と反比例」は基本を理解し、関係式を覚えておけば、それほど難しくはない単元です。
大切なことは、たくさんの問題に取り組み解き方に慣れておくことです。
「比例と反比例」に苦手意識がある人や、数学をもっと勉強したいという人は、ぜひ一度気軽に個別指導WAMにご相談ください。
個別指導WAMでは、学習全般のサポートをさせていただきます^^